

Some people have asked me about converting between latitude/longitude & Ordnance Survey grid references. The maths seems extraordinarily complex (and way beyond me!), but the Ordnance Survey explain the resulting formulae very clearly in Annex C of their Guide to coordinate systems in Great Britain.

OS Grid References are based on 100km grid squares identified by letter-pairs, followed by digits which identify a sub-square within the grid square, as explained on the OS Interactive Guide to the National Grid. 6-digit references identify 100m grid squares; 8 digits identify 10m grid squares, and 10 digits identify 1m squares. TG51401317 represents a 10m box with its (south-west) origin 51.40km across, 13.17km up within the TG square.
An alternative way of expressing OS Grid References is as all-numeric eastings and northings, usually in metres. As square TG is six squares across, three squares up within the grid, grid reference TG 5140 1317 can also be expressed as 651400,313170.
As the surface of the earth is curved, and maps are flat, mapping involves a projection of the (ellipsoidal) curved surface onto a (plane) flat surface. The Ordnance Survey grid is a transverse Mercator projection.
Before I started writing these geodesy scripts, I assumed a latitude/longitude point was a latitude/longitude point, and that was that. Since then, I have discovered that if you’re being accurate, things get more complicated, and you need to know what datum you are working within.
Historically, cartographers worked at finding the ellipsoid which provided the closest mapping to the local geoid. The geoid is equivalent to the local mean-sea-level (or its equivalent in land-locked locales), and is determined by the local force of gravity. These ellipsoids were then fixed to local datums (fixed reference frames established through cartographic surveys). Simplifying enormously, this approach has now been broadly replaced by global geocentric ellipsoids fixed to global & continental datums (or reference frames) which can be readily mapped to each other to account for tectonic plate shifts. The best known global datum is WGS84, which is used by GPS systems; its more accurate siblings are (date-dependant) ITRFs. Continental datums include NAD-83 for North America, ETRS89 for Europe, GDA94 for Australia, etc.
Back in the 1930’s, the UK Ordnance Survey defined ‘OSGB-36’ as the datum for the UK, based on the ‘Airy 1830’ ellipsoid. In 2014, they deprecated OSGB-36 in favour of WGS-84 for latitude/longitude coordinates, but OSGB-36 is still the basis for OS grid references. The Greenwich Observatory – historically the ‘prime meridian’ – is around 000°00′05″W on the WGS-84 datum (a difference of a bit over 100 metres): and moving every year. (I find the history of cartography facinating: I will put together a reading list sometime).
So to convert a (WGS84) latitude/longitude point to an OS grid reference, it must first be converted from the WGS84 datum to the OSGB36 datum, then have the transverse Mercator projection applied to transform it from a curved surface to a flat one.
To convert between datums, a ‘Helmert transformation’ is used. The Ordnance Survey explain the details in section 6 (and the annexes) of their Guide to coordinate systems in Great Britain.
The procedure is:
1 convert (geodetic) latitude/longitude to geocentric cartesian coordinates:
| e² = (a²−b²) / a² | eccentricity of source ellipsoid (= 2·f − f²) |
| ν = a / √(1 − e² · sin²φ) | transverse radius of curvature |
| x = (ν+h) · cosφ · cosλ | |
| y = (ν+h) · cosφ · sinλ | |
| z = ((1−e²)·ν + h) · sinφ |
2 apply Helmert transform
The 7-parameter Helmert transform is given by:
| x | ′ | tx | 1+s | −rz | ry | x | |||||||||||
| y | = | ty | + | rz | 1+s | −rx | · | y | |||||||||
| z | tz | −ry | rx | 1+s | z |
Hence:
| x′ = tx + (1+s)·x − rz·y + ry·z | |
| y′ = ty + rz·x + (1+s)·y − rx·z | |
| z′ = tz − ry·x + rx·y + (1+s)·z |
3 convert cartesian co-ordinates back to latitude/longitude
While the conversion from geodetic to cartesian is straightforward, converting cartesian to geodetic is a complex problem.
There are a number of possible approaches: this uses Bowring’s 1985 method (The Accuracy of Geodetic Latitude and Height Equations – Survey Review Vol 28, 218, Oct 1985), which provides approximately μm precision on the earth ellipsoid, in a concise formulation. If you have more demanding requirements, you could compare e.g. Fukushima (2006), Vermeille (2011), Karney (2012), and others.
| e² = (a²−b²) / a² | 1st eccentricity of ellipsoid (= 2·f − f²) | |
| ε² = (a²−b²) / b² | 2nd eccentricity of ellipsoid (= e² / (1−e²)) | |
| ν = a / √(1 − e² · sin²φ) | length of normal terminated by minor axis | |
| p = √(x² + y²) | distance from minor axis | |
| R = √(p² + z²) | polar radius | |
| tanβ = (b·z)/(a·p) · (1 + ε² · b/R) | parametric latitude | (17) |
| tanφ = (z + ε²·b·sin³β) / (p − e²·a·cos³β) | geodetic latitude | (18) |
| tanλ = y / x | longitude | |
| h = p·cosφ + z·sinφ − a²/ν | height above ellipsoid | (7) |
Accuracy: the Ordnance Survey say a single Helmert transformation between WGS84 and OSGB36 is accurate to within about 4–5 metres – for greater accuracy, a ‘rubber-sheet’ style transformation, which takes into account distortions in the ‘terrestrial reference frame’ (TRF), must be used (‘OSTN02’ ‘OSTN15’): this is a different level of complexity, if you require such accuracy, I expect you already know more about OSGB transformations than me.
With the latitude/longitude in the OSGB-36 datum, a transverse Mercator projection is then applied to obtain a rectilinear grid. The OSGB uses the Lee–Redfearn implementation of the Gauss–Krüger projection.
The OSGB national grid uses a true origin of 49°N, 2°W. A false origin of −100 km north, 400 km east is then applied, so that eastings are always positive, and northings do not exceed 1,000 km.
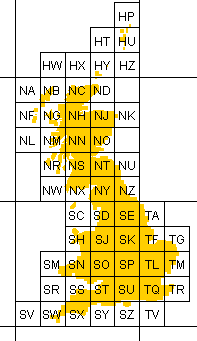

Aside from the transformation maths, the other tricky bit of the script is converting grid letter-pairs to/from numeric eastings & northings. To follow what’s going on, it is worth noting that the letter-pairs define a 5x5 grid of 500km squares, each containing 5x5 sub-grids of 100km squares; the eastings & northings work from a ‘false origin’ at grid square SV, which is displaced from grid square AA by 10 squares E, 19 squares N, with the northing axis inverted; and letter ‘I’ is skipped.
OSGB Grid References apply to Great Britain only (Ireland and the Channel Islands have separate references).
To convert an Ordnance Survey grid reference to a (WGS-84) latitude/longitude point:
<script type="module">
import OsGridRef from 'https://cdn.jsdelivr.net/npm/geodesy@2/osgridref.js';
const gridref = OsGridRef.parse('TL 44982 57869');
const wgs84 = gridref.toLatLon();
console.log(wgs84.toString('d', 2)); // '52.20°N, 000.12°E'
</script>
To convert a (WGS-84) latitude/longitude point to an Ordnance Survey grid reference:
<script type="module">
import { LatLon } from 'https://cdn.jsdelivr.net/npm/geodesy@2/osgridref.js';
const wgs84 = new LatLon(52.2, 0.12);
const gridref = wgs84.toOsGrid();
console.log(gridref.toString()); // 'TL 44982 57869'
</script>
See documentation for full details.
Distances between OS grid reference points are straightforward to calculate by pythagoras, once references are converted to numeric form. For UTM coordinates & MGRS grid references, see my UTM-MGRS page. For other scripts for calculating distances, bearings, etc between latitude/longitude points, see my Lat/Long page.
See below for the JavaScript source code of the transverse Mercator projection and the datum transformation, also available on GitHub. Full documentation is available, as well as a test suite.
Note I use Greek letters in variables representing maths symbols conventionally presented as Greek letters:
I value the great benefit in legibility over the minor inconvenience in typing (if you
encounter any problems, ensure your <head> includes <meta charset="utf-8">,
and use UTF-8 encoding when saving files).
With its untyped C-style syntax, JavaScript reads remarkably close to pseudo-code: exposing the algorithms with a minimum of syntactic distractions. These functions should be simple to translate into other languages if required, though can also be used as-is in browsers and Node.js.
For convenience & clarity, I have extended the base JavaScript Number object with
toRadians() and toDegrees() methods: I don’t see great likelihood of
conflicts, as these are ubiquitous operations.
 I offer these scripts for free use and adaptation to balance my debt to the open-source info-verse.
You are welcome to re-use these scripts [under an MIT licence,
without any warranty express or implied] provided solely that you retain my copyright notice and a link to this page.
I offer these scripts for free use and adaptation to balance my debt to the open-source info-verse.
You are welcome to re-use these scripts [under an MIT licence,
without any warranty express or implied] provided solely that you retain my copyright notice and a link to this page.
If you need any advice or development work done, I am available for consultancy.
If you have any queries or find any problems, contact me at ku.oc.epyt-elbavom@oeg-stpircs.
© 2002-2022 Chris Veness